Spring 2000
Revised and edited for the web March 2004
www.integralscience.org
Also, in the Christian tradition it is said that all things arise from a sacred Word. In the Gospel According to John, for example, it is said
IIn the beginning was the Word, and the Word was with God, and the Word was God. The same was in the beginning with God. All things were made by it; and without it was not any thing made that was made.
IAnd Meister Eckhart adds,
If God stopped saying his Word, but for an instant even, heaven and earth would disappear.
It is also the act of divine speech in Genesis that brings heaven and earth into existence. Creation is thus “the Word made flesh” through the act of divine poetry. The Greek word poesis (related to our words poetry and poem) means simply making or creating. The divine poetry is thus the divine creation, which is the world. And the Greek word logos (related to our words logic, analogy, and dialogue) is also the divine Word by which all things were made. The logos of poesis is both the “logic of poetry” as well as the seed syllable or word at the root of all creation. Here we have the first hint of a deep connection between the logic of mathematics and the poetics of enlightenment. Perhaps there is more than just an etymological connection between the logic that is fundamental to mathematics and the logos that some traditions say is fundamental to all creation. The remarkable effectiveness of mathematics in the physical sciences suggests that there is, indeed, a deep connection between the manifested world and this logos, or fundamental vibration, that is involved in the poesis of all form.
Because the archetypal numerical principles are common to the cosmos as well as the psyche, these numbers are not inert abstractions but active powers. For example, it is said that Pythagoras used the principles of numbers to heal the soul through the medium of music. The harmonies of music resonate with corresponding parts of the soul, bringing the soul into harmony with itself. The healthy soul is the soul that is resonating with the harmony of the cosmos. Pythagoras also taught that the soul can resonate with the divine principles of the cosmos through direct contemplation of mathematical truths of numbers. As music and art bring harmony to the soul through the senses of hearing (time) and seeing (space), mathematics brings harmony to the soul through the intellect (number). Indeed, the Greek word theorem means something to contemplate or behold. The most sacred symbol of mathematical contemplation in the Pythagorean tradition is the tetraktys, which consists of the first four numbers arranged in a triangle of ten points:
o 1
o o 2
o o o 3
o o o o 4
The tetraktys represents various important aspects of the numerical principles and their manifestation. For example, the ratios of the adjacent rows give the fundamental musical harmonies, 1:2 (octave), 2:3 (fifth), and 3:4 (fourth). The tetraktys is also a symbol of cosmogenesis. From the original undifferentiated One the principle of Duality manifests. From these two principles of the One and the Many, the principles of the Trinity and Quaternary are generated. The Trinity brings harmony to the One and the Many, while the Quaternary brings completion to the harmony. These four principles, in turn, provide the archetypal patterns for further manifestation (e.g., the generation of all the notes in the musical scale). This cosmogenesis is also manifested in geometric or spatial terms. One represents a single point; Two represents a pair of points forming a line; Three gives a triangle; and Four generates a tetrahedron, the basic three-dimensional material element. The tetraktys also has the significant property that the total number of points is ten (1+2+3+4=10), a number representing unity. Contemplation of this symbol brings the soul into harmony with the ordering principles of manifestation, the logos of divine poesis.
Each thing hath two faces, a face of its own, and a face of its Lord; in respect of its own face it is nothingness, and in respect of the Face of God it is Being. Thus there is nothing in existence save only God and His Face.
A similar teaching is found in the Buddhist tradition. A thing’s “face of its own” is its form, which is empty of any independent existence. A thing’s “face of its Lord” is its ultimate nature, which is not other than its form. All form is empty, and emptiness is nowhere other than in the forms themselves. In particular, words and symbols are understood in these traditions to be not separate from the ground from which they come. For example, spoken words are the articulations of the movement of breath, or spirit. But, like waves on the ocean, these apparent interruptions of the breath are not separate from the breath. Sound and silence are two aspects of the same flow, just as God’s manifest and unmanifest aspects are ultimately not separate, just as form and emptiness are not separate.
We say that the one and many become identified by thought, and that now, as in time past, they run about together, in and out of every word which is uttered, and that this union of them...[is] an everlasting quality of thought itself, which never grows old (Philebus, 15D).
In his Commentary on Plato’s Parmenides, the Neoplatonist Proclus adds,
The cosmos is not a unity here and a plurality there, but a unity and a plurality at the same time throughout its whole being...and there is nothing you can take within it that is not both one and many.
Although this coincidence of the One and the Many is illogical (indeed, it violates Aristotelian logic to identify opposites), it expresses the paradoxical essence of logos, the archetype of relationship and mediation. Consider, for example, a circle drawn in a plane:

On the one hand, this circle separates, or divides the inside from the outside, expressing the principle of Many. On the other hand, however, the circle also connects and binds the inside and outside together, expressing the principle of One. The circle can be viewed either way. The One and the Many are both simultaneously present in this elementary geometrical symbol. Analogously, all forms have both their own face (symbolizing the Many), and the face of their Lord (symbolizing the One).
This coincidence of the One and the Many is essential to both musical harmony and geometrical symmetry. For example, two tones having the mathematical ratio 1:2 are manifestations of the same note in different octaves. On the one hand, if the two notes were the same in all respects and had a trivial ratio of 1:1, there would be no harmony. Harmony requires difference. On the other hand, if the two notes were so different that they had no simple ratio, they would not harmonize. Thus, harmony requires the simultaneous presence of both sameness and difference, both One and Many. Similarly, consider the spatial symmetry of a square.

The sense of beauty in the symmetry of the square derives from the fact that the four sides are the same, and yet different. On the one hand, if the four sides were absolutely identical, they would overlap and reduce to a single line. The four sides must have distinct positions for the square, and its symmetry, to be formed at all. On the other hand, if the four sides were entirely different, they would have different lengths, and would be joined at different angles with respect to each other. In this case also there would be no square, and no symmetry. Like musical harmony, the beauty of geometric symmetry requires that there be a simultaneous presence of both similarity and difference, both One and Many.
In God we must not conceive of distinction and indistinction, for example, as two contradictories, but we must conceive of them as antecedently existing in their own most simple beginning, where distinction is not other than indistinction (Cusa, 1997).
Cusa recognized that the coincidence of opposites is an expression of the principle of Incarnation, wherein God’s identification with creation in Jesus coincides with God’s transcendence above all creation. In God the opposites of identity and difference coincide. Thus Cusa presents a conception in which the ineffability of the Infinite coincides with its expressibility in the finite, in which creator coincides with creation, transcendent coincides with immanent, and One coincides with Many. Cusa says in De Docta Ignorantia that the best way to evoke these mystical insights is through mathematical symbols:
Since there is no other approach to a knowledge of things divine than that of symbols, we cannot do better than use mathematical signs on account of their indestructible certitude (Cusa, 1997).
For example, Cusa compared the relationship between the finite, discursive intellect and the infinite Truth to the relationship between a polygon and a circle:
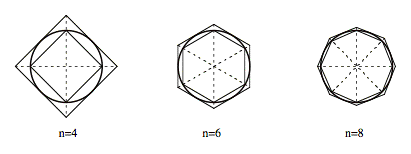
For the intellect is to truth as an inscribed polygon is the inscribing circle (Cusa, 1985).
As the number of sides to the polygon increases, it more closely approximates the circle. But no polygon actually coincides with the circle. The polygon and the circle only coincide when the number of sides of the polygon is actually infinite. Such a polygon, however, is inconceivable to the rational mind. Yet, this mathematical symbol evokes a sense of connection between the conceivable and the inconceivable, a way to approach the divine through its representations in finite forms. As the number of sides to the polygon becomes infinite, the rational mind fails, opening awareness up to something beyond, where the infinite sides of the polygon (the Many) coincide with the perfect continuity of the circle (the One).
The Absolute can only be acknowledged and admitted, never known, not even approximately (quoted in Hallett, 1984).
The Infinite remains at the border comprehensibility, inviting us with its paradoxes to transcend the apparent division between finite and Infinite. As Nicholas of Cusa closes his treatise on learned ignorance,
These profound matters should be the subject of all the effort of our human intelligence, so that it may raise itself to that simplicity where contradictories coincide (Cusa, 1997).
In the 20th century, Hilbert, Russell and other mathematicians attempted to eliminate the paradoxes of set theory, so that mathematics would have a consistent and completely rational foundation. This program, however, was shown to be impossible by Kurt Gödel. Mathematics can never be completely reduced to an explicit set of axioms and logical rules. Any such attempt to fix mathematics in this way will always leave an inexplicable remainder. The mathematical system will leave out certain truths, it will be incomplete. Like Cusa’s polygons, it must either fall short of the completeness of the circle, or embrace the paradoxes of the infinite.
It is remarkable that Gödel’s proof of the incompleteness of any axiomatic system is based on a modern application of the ancient identity between numbers and letters. In Gödel’s proof, each letter or symbol used in a mathematical statement (e.g., a, b, c, =, +, -) corresponds to a unique number (e.g., 1, 2, 3, 4, 5, 6). These numbers can then be used to assign a unique number to each mathematical statement. For example, the symbols in “a+b=c” correspond to the sequence {1, 5, 2, 4, 3}. The first five prime numbers are then raised to these exponents and multiplied together to yield the unique number: 21 35 52 74 113=38,828,131,650. This number is unique because every number has a unique prime factorization. Moreover, this correspondence between statements about numbers and numbers themselves also relates logical relationships between mathematical statements to arithmetical relationships between numbers. A true mathematical proposition in the system thus corresponds to a true arithmetical relationship of numbers. This correspondence between levels of language allowed Gödel to construct a self-referential statement G=“this statement is not provable within the system”. Now consider whether or not G is true. Suppose that G is false. Then, since false statements are not provable by a logically consistent system, G is not provable by the system. So, if G is false, then G is not provable by the system. But G says that G is not provable by the system; so if G is false, then G is in fact true. This contradiction means that G cannot be false, as supposed. So G must be true, i.e., it is true that the statement G is not provable by the system, just as G says. Thus, G is true, but the system cannot prove it. In other words, if the system is consistent, then it is incomplete. Conversely, if the system is complete, then it must be inconsistent. The conclusion is that the mathematical system is either inconsistent or incomplete. In other words, axiomatic mathematical systems must either surrender the absolute distinction between true and false, or must surrender their claims to being totalizing accounts of truth.
Gödel showed that truth cannot be contained within the limits of strict logic. Only if we allow paradox can truth completely reveal itself in form. These two sides of Gödel’s proof represent the apophatic (via negativa) and cataphatic (via positiva) approaches to truth, respectively. In the apophatic approach, one adheres to strict logic to show that any attempt to represent or speak of truth necessarily fails—the truth is beyond all rational comprehension. In the cataphatic approach, on the other hand, one embraces paradox and the coincidence of opposites to demonstrate the tangible presence of truth in all its limitless expressions. Like the ancient mathematics of Pythagoras, Gödel’s mathematical proof can be seen as a symbol of profound truths about the relationship between the limited and the unlimited, form and formlessness, transcendence and immanence. Gödel’s postmodern mathematics undermines any attempt to fixate on any totalizing axiomatic system for mathematical discourse, and reveals the essential ambiguity, openness, and emptiness of mathematical activity.
Wolff suggested that one important reason to expect that mathematics should be especially useful in expressing subtle non-conceptual cognitions is its universality and invariance:
The universal...is in closer affinity to the Illuminative cognition than is the particular. ...Since it is from the general or universal concepts that the largest deductive development is possible, it follows that a philosophy grounded on the Illuminative Cognition would elaborate itself mainly as a deductive system. ...Here we can see the possibility of a mathematic which is a revelation of truth (Wolff, 1995).
Pure mathematics is the only real invariant that we have in the ever-changing phantasmagoria of experience. ...The law that governs the flow of consequences [in a mathematical system] is tougher than tempered steel and harder than the hardest rock. Save in the Self, here, as nowhere else, is there something to which human consciousness may tie and give its trust...and this invulnerable core carries straight through to Consciousness-Without-An-Object (Wolff, 1994).
Mathematics is a bridge to the Transcendent, an image in form of the universal and absolute ground of form, a symbolic language that can reveal or translate the subtle, or “higher”, conscious experiences into form. Wolff recognizes, however, that this translation can never be perfect or complete:
The immediate content of the Higher Consciousness cannot be cross-translated, but certain formal properties can be through the use of systematic symbols. ...In fact, if the consciousness-equivalents of the entities and operations of pure mathematics were realized, we would find that, in that great science and art, cross-translation in a lofty sense already exists (Wolff, 1994).
Mathematics, in other words, already contains the formal language to express many of the subtle structures of inner experience—we need only discover the correlations between them, the mathematical correlates of enlightened experience. Like a pure Pythagorean, Wolff recognizes that mathematics is a poetics of enlightenment, a unique and powerful expression of divine reality. Modern mathematics, however, has gone far beyond the mathematics of Pythagoras. We now have not only positive integers, but also zero, negative integers, rationals, irrationals, transcendentals, imaginary numbers, quaternions, matrices, transfinite numbers, etc. We now have not only Euclidean geometry, but also non-Euclidean geometries, projective geometry, differential manifolds, topology, set theory, etc. If the power of modern mathematics in 20th century physics is any indication of its inner depths, a modern mathematical poetics may find an important place in Western enlightenment traditions of the future. What might this look like? Let us take a closer look at some of Wolff’s mathematical poetics.
Wolff uses mathematical symbols themselves to express aspects of how mathematical symbols can be used as a bridge to “cross-translate” between Transcendent and relative realms of consciousness. Although abstract mathematical concepts are excellent vehicles for carrying transcendent values, they are, if taken at face value, objects in the relative world and can therefore never completely convey the non-relative content of transcendent states. As Wolff explains,
There is an irreducible incommensurability which forever makes correct cross-translation impossible. ...Still, there is such a thing as approximation to cross-translation in much the sense that a mathematician can give an approximate rational evaluation of an irrational number, such as the square root of two (Wolff, 1994).
To completely cross-translate the square root of two would mean to completely specify all the digits of its decimal expansion; but its decimal expansion has an infinite number of digits with no repeating pattern; thus to completely specify all the digits in its decimal expansion is impossible, just as Cusa’s polygons never actually become a circle. It is the same, Wolff says, with attempts to consistently and completely express the transcendent within the bounds of the relative world.
Wolff repeatedly uses mathematical symbols and metaphors where conventional language seems to fail. His most frequently used mathematical symbols are Infinity, Space, Point, and Zero. Infinity was most notably used in reference to what he calls the High Indifference.
Just as in mathematics there are infinitudes of higher orders infinitely transcending lower infinities, so it is in the Transcendent World. ...I have found an Infinite World, and then another Infinite consuming the first. ...It is an Infinity of some higher order, that is an INFINITY which comprehends lesser Infinities. (Wolff, 1994).
Here Wolff refers to Cantor's mathematical theory of transfinite numbers. In his famous diagonalization argument, Cantor proves that one transfinite number can be larger than another, in particular, that the infinite number of points on the real number line between zero and one is greater than the infinite number of positive integers. The proof begins by supposing that these two infinite numbers are equal, i.e. that the points on the number line can be put in one-to-one correspondence with the positive integers. If, as supposed, we can number each point with a positive integer, then we can make a sequential list of all the points (in no particular order), writing the decimal expansion of each real number next to its corresponding positive integer. For example,
1 0.029384710 ...
2 0.470128374 ...
3 0.234928702 ...
4 0.872938472 ...
5 0.295629056 ...
etc.
By supposition, this list completely enumerates every real number. Yet it is not complete since there are numbers not on the list. For example, construct a number that has its first digit different from the first digit of the first number, its second digit different from the second digit of the second number, its third digit different from the third digit of the third number, and so on. This will result in a unique number that differs from every number on the list and yet it specifies a point on the real number line. Therefore, the number of points on the real number line must be greater than the number of positive integers. Since both numbers are infinite, there are thus two infinities of different magnitudes. The infinity of the positive integers is called a countable infinity, while the larger infinity of the continuum of real numbers is called an uncountable infinity. Wolff’s first transcendental realization is symbolized by the countable infinity that is greater than any finite number. Because the second transcendental realization, the High Indifference, transcended the first, it is symbolized by the larger, uncountable infinity of the continuum.
In addition to the Infinite, Wolff also uses zero as a significant symbol. In its first sense, Wolff uses zero as a symbol for the Self stripped of all objects.
Here we have a notion which stands for nothing, and yet becomes the most vital unifying conception of mathematics. ...Upon zero we build our systems of reference, which is merely a way of saying that with nothing as a center we have the fulcrum for control of all elaborations in form. ...The pure ‘I’ is the zero-point of organized consciousness (Wolff, 1995).
In transcendental realization, this bare point-I is then transformed into the Space-I. The Self is as much a space as a point, symbolized by both zero and Infinity. Yet in the High Indifference, even this Self vanishes, leaving only Consciousness-Without-An-Object (and Without-A-Subject).
Consciousness-Without-An-Object is the universal solvent within which the centers of tension, or objects, have their field of play. All tendency in that play is counter-balanced by its counter-tendency, the culminating effect being an expression equated to zero. It is zero that symbolizes the durable Reality, or Consciousness-Without-An-Object” (Wolff, 1994).
This is the higher sense of zero, symbolizing the cancellation of the positive and negative polarizations of primordial awareness, and the absence of even the transcendent Self in a Great Space beyond and comprehending all opposites.
Part of the power of abstract mathematical symbols is their near-incomprehensibility, their subtle dance at the edge of form that allows the formless to transparently shine through. When the mind clings to their objective form, they are opaque to Transcendent meaning. But when the mind relaxes and opens to their non-objective transparency, the meaning floods in. Wolff coined the term ‘inverse cognitions’ to describe cognitions polarized in the opposite sense as objective cognitions, i.e., “axial” cognitions that “turn about” from form to formlessness.
Awareness of the absence of objects, in its purity, is not a cognition of an object, but another form of consciousness that is not concerned with objects. However, a reflection of this state of consciousness may be produced so that a special cognition arises, of such a nature that its content is definable as the inverse of all objects...illustrated very well in mathematics in connection with the development of the notions of negative, imaginary, infinitesimal, and transfinite numbers. All these may be regarded as of the nature of inverse cognitions (Wolff, 1994).
It is true that man has arrived at the notion of continuity, although...he never really thinks it. ...Continuity belongs to the hinterland of Consciousness. This simply illustrates the eternal fact, i.e. that the actual consciousness of man continually operates in a Nirvanic as well as in a Sangsaric sense (Wolff, 1994).
Thus these inverse cognitions found in mathematics are profound vehicles for recognizing the Nirvanic pole of consciousness, for seeing both the face of the symbol and the face of the Lord, the Many and the One.
The conceptions of negative, imaginary, infinitesimal, and transfinite numbers, as well as the conception of the continuum, are all symbols for inverse cognitions by virtue of their common transcendence of the conventional universe of positive integers. We have already seen how the infinity of the continuum transcends the infinity of positive integers with respect to the size of the infinities present in each type of number. The transcendence, however, is also a transcendence of the kind of number, and not merely the size. It is a liberation not only from quantitative bounds, but also from qualitative bounds into new forms of number having more universal laws. The development of mathematics, in other words, illustrates the rupturing of previous limited conceptions and forms, opening up into subtler kinds of order. For example, within the bounds of positive integers the laws of subtraction are limited by the requirement that the result must be positive. With the birth of the conception of negative number, however, no such limits need be imposed upon the laws of subtraction. Similarly, within the bounds of real numbers the laws for taking square roots must be restricted by the requirement that square roots may only be taken of positive numbers. With the birth of imaginary numbers, however, no such limits need be imposed. Similarly, in the case of transfinite numbers the laws become even less restrictive. What was impossible with finite numbers before is now possible with infinite numbers. For example, a transfinite number can be divided in two without decreasing in size (e.g., there is a countable infinity of even numbers, even though they represent only half of all the positive integers). These new forms of number thus symbolize modes of consciousness where the restrictive forms of our conventional universe are transcended, where the impossible becomes the possible, and where new forms of reality are realized where there was apparently nothing before.
Man will have long since ceased to be human, in the restricting meaning of the term, by the time he has awakened in terms of Consciousness at the most advanced levels represented by mathematical concepts and symbolic formulae. Mathematics thus constitutes a thread to the Beyond that has never been lost (Wolff, 1994).
The ‘eye’ of the mathematician actually sees into the deep structure of the subjective psyche. ...May it not be that the mathematical thought is the speech of the Divinity in the inner consciousness of man? Then the mathematical thought is inner communion (Wolff, 1995).
For him who penetrates deeply into the roots of logic itself, the Recognition can be aroused. ...Let a man unveil this Recognition and make It immediately and consciously his own, and then he will find in logic a power which, if followed with a single eye, will take him through to the Higher Consciousness (Wolff, 1994).
Like Pythagoras, Wolff knew mathematics to be not only a thread by which we may know the Beyond, but also a means by which we may Know it.
Although it may be plausible that mathematics could serve to transform our fixed modes of consciousness, how are these mathematical symbols used to assist the contemplative in developing non-conceptual insights? What are the guidelines for practicing this mathematical yoga? Wolff gives us various pointers and suggestions regarding how mathematics might be implemented as a yoga.
It is possible to take the symbol itself as an object of thought and use it for the purposes of philosophical and general mystical integration. ...There is some reason to believe that such a method of procedure is possible within the setting of Western culture. ...This possibility I see as growing out of our peculiar mathematical development. (Wolff, 1973)
The particular meaning carried by specific mathematical symbols can be revealed through contemplation, bringing illumination into the mind via the symbol. Mathematics is also of service to the contemplative by virtue of its inherent abstractness, rather than due to the particular meaning associated with its symbols.
The greatest achievement of western genius has been in the development of the abstract thought which has its crown in higher mathematics. The freeing of thought from dependence upon the sensible image is an accomplishment of the very greatest difficulty. Until thought has won this power, it cannot penetrate into the Realm of Imageless Consciousness. Now, once it is realized how much has been accomplished in this direction in the field of higher mathematics, it is easy to see what a powerful instrument in the practice of Dhyana we have forged. (Wolff, 1944)
A significant part of the transformative power of mathematics, in other words, is to train the attention to free itself from fixation on concrete objects of consciousness, and on fixed perspectives in consciousness. Wolff testifies that mathematics used in this way was a powerful method for training his own mind:
In my own experience, thought on the level of Imageless Consciousness was possible by employing the intellectual capacities unfolded during the years of mathematical discipline. (Wolff, 1944)
Wolff also testifies that the discipline of mathematics helps to purify the mind because
in the cognitive activity of pure mathematics...the desire is almost wholly directed toward Truth and Beauty, with little or no attachment to any preconception of what Truth may ultimately prove to be. Cognitive activity of this type...may well prove to be one of the most powerful subsidiary aids for those who can make use of it. (Wolff, 1944)
This purification of the mind is directly related to the capacity to clearly observe inner experience in stable balance of subtle attention. As Wolff goes on to explain,
The validity of mathematics is established upon a basis that is quite impersonal and universal. ...In its purity it deals only with transcendental or ideal objects of the very highest order of thinkable abstraction or universality. In high degree, the consciousness of the mathematician qua mathematician is not concerned with either a self or objects...in higher degree than anywhere else, except perhaps in states of samadhi of a high order. Herein is revealed the power of pure mathematics as an instrument of consciousness-transformation on a very lofty level. (Wolff, 1973)
The transformative power of mathematics, however, is not derived from its noetic component alone. There is also an essential affective and aesthetic component. Without this heart and soul of mathematics, it is empty of any transformative power.
Without the Recognition of Soul, in some sense, such as the soul of mathematics or of logic or in some other form, formal demonstration proves merely possibility or the hypothetical imperative but never arrives at the categorical imperative. The only knowledge that can possibly Liberate man is categorical” (Wolff, 1994).
Thus the transformative power of mathematics lies not just in its abstract form and logic, but in its soul where it is felt with the heart. The logical harmony of mathematics is a vehicle for a deeper meaning that resonates with the hidden parts of the soul. The logos of mathematics is not just its order, but also its meaning; not just its quantity but also its quality. Indeed, Wolff points out in regard to the use of mathematical symbols for spiritual transformation, that
to step from the symbol to that which is symbolized, though this does afford a peculiarly exacting demand upon acuity of thought, yet requires much more. Here, feeling, in the best sense, must fuse with thought. The thinker must learn also to feel his thought, so that, in the highest degree, he thinks devotedly. It is not enough to think clearly, if the thinker stands aloof, not giving himself with his thought. The thinker arrives by surrendering himself to Truth, claiming for himself no rights save those that Truth herself bestows upon him. In the final state of perfection, he possesses no longer opinions of his own nor any private preference. Then Truth possesses him, not he, Truth. He who would become one with the Eternal must first learn to be humble. He must offer, upon the sacrificial alter, the pride of the knower. He must become one who lays no possessive claim to knowledge or wisdom. This is the state of the mystic ignorance — of the emptied heart (Wolff, 1994).
Thus the transformation of the heart is an essential part of the method which employs mathematics for spiritual realization. The mere logical manipulation of symbols, as secular mathematics is often practiced, is impotent as a transformative practice. Mathematical poetics is not some dry, heartless churning of the rational mind. It is as full of heartfelt meaning as any other enlightened poetics. In addition, mathematics can itself aid in this heart transformation by virtue of its embodiment of Truth in a particularly pure form. Mathematics thus provides an excellent object of devotion, if we choose to regard it as such. This played an important role on Wolff's path of transformation.
A desire for the transcendent Self and a love of universals also tend toward the required melting of the egoistic feeling. In this part of the discipline I found that my already established love of mathematics and philosophy was an aid of radical importance (Wolff, 1994).
In the cognitive activity of pure mathematics...the desire is almost wholly directed toward Truth and Beauty, with little or no attachment to any preconception of what Truth may ultimately prove to be. Cognitive activity of this type...may well prove to be one of the most powerful subsidiary aids for those who can make use of it (Wolff, 1994).
The essential key to employing mathematics as an effective transformative discipline, then, lies in the heart we put into it, the purity of our intention:
The two great factors which implement the motivation underlying the drive toward Mystical Realization are (1) Love of Truth, and (2) Compassion. ...Compassion and the Love of Truth are the only valid and effective motivations, and the Compassion must be utterly self-disregarding, and the seeking of Truth must be so pure that every preconception is offered up on the alter of sacrifice (Wolff, 1995).
One can raise a study [of mathematics] to the status of an effective transforming agent only by giving himself to it with the same completeness that is characteristic of the more intense religious natures. ...It is just the subtle change implied in the difference between secular and sacred which makes all the difference in the world. In principle, anything whatsoever can acquire the sacred value; it is simply important that the attitude of sacredness shall exist and shall absorb the predominant portion of the interest. Sacredness implies self-giving, while secularity implies self-withholding. In the transformative process, everything else is incidental to the attaining of the self-giving attitude (Wolff, 1995).
Mathematical poetics, when practiced with great devotion and humility, necessarily involves the transformation of both mind and heart and inevitably involves both wisdom and compassion. In essence, it is like any enlightened poetics, combining the principles of One and Many, both revealing and veiling. Its logos manifests as numerical proportion, vibrational harmony, geometrical symmetry, and cosmic order. Enlightened poesis is the radiant creativity, the translucent manifestation that is not other than the radiance itself. May we all know and be it.
Dyczkowski, (1992), The Stanzas on Vibration (Albany : SUNY Press).
Guthrie, Kenneth S. (1987), The Pythagorean Sourcebook and Library (Grand Rapids, MI : Phanes Press).
Hallett, Michael (1984), Cantorian Set Theory and Limitation of Size (Oxford: Oxford University Press).
Nicholas of Cusa (1985), Nicholas of Cusa on Learned Ignorance: A Translation and an Appraisal of De Docta Ignorantia, Hopkins, Jasper, tr. (Minneapolis: The Arthur J. Banning Press).
Nicholas of Cusa (1997), Nicholas of Cusa: Selected Spiritual Writings, H. Lawrence Bond, tr., (New York: Paulist Press).
Rucker, Rudy (1983), Infinity and the Mind (New York: Bantam Books). Schimmel, Annemarie (1993), The Mystery of Numbers (New York : Oxford University Press).
Sells, Michael A. (1994), Mystical Languages of Unsaying (Chicago : University of Chicago Press).
Spencer-Brown, G. (1969), Laws of Form (London: George Allen and Unwin).
Wolff, F. (1944) [Merrell-Wolff, F.], Pathways Through to Space (New York: Richard R. Smith); reprinted in Merrell-Wolff, F. (1994).
Wolff, F. (1973) [Merrell-Wolff, F.], The Philosophy of Consciousness Without An Object (New York: Julian Press); reprinted in Merrell-Wolff, F. (1994).
Wolff, F. (1994) [Merrell-Wolff, F.], Experience and Philosophy: A Personal Record of Transformation and a Discussion of Transcendental Consciousness (Albany, NY: SUNY Press).
Wolff, F. (1995) [Merrell-Wolff, F.], Transformations in Consciousness: The Metaphysics and Epistemology (Albany, NY: SUNY Press).
(c) 2000 Thomas J McFarlane