www.integralscience.org
This essay presents Merrell-Wolff's writings on the spiritual function of mathematics, selected from his three major works, Pathways Through To Space, The Philosophy of Consciousness Without An Object, and Introceptualism. Mathematics, according to Wolff, functions as a bridge between the relative and transcendent states of consciousness. It serves, on the one hand, as a vehicle for crossing from the transcendent to the relative by providing a highly subtle and precise language for expressing the immediate contents of transcendent states with minimal distortion. On the other hand, it also serves as a vehicle for crossing from the relative to the transcendent by providing highly abstract and universal symbols for generating insights through contemplation. Wolff emphasizes, however, that although the structure of this mathematical bridge is provided by the highly subtle forms of thought, an actual crossing of the bridge requires the motivating power of love and devotion.
Wolff calls the expression of the content of transcendent states in the forms of relative thought the process of cross-translation. "The immediate content of the Higher Consciousness can not be cross- translated, but certain formal properties can be through the use of systematic symbols. . .In fact, if the consciousness- equivalents of the entities and operations of pure mathematics were realized, we would find that, in that great science and art, cross- translation in a lofty sense already exists."[51] Yet Wolff acknowledges that cross- translation is not a trivial task, for the Higher Consciousness "is not an easy Sea in which to think, when one tries to retain correlation with the outer consciousness. Whatever success I do attain in navigating in this compound of the Sea and relative consciousness, I owe very largely to the years of training in higher mathematics."[52]
But why should mathematics be so well suited for this task of cross- translation? Put simply, it is because "our most abstract language is the best vehicle of ultimate truth."[53] This is an immediate consequence of Wolff's fundamental principle that substantiality is inversely proportional to ponderability.[54] "The universal. . .is in closer affinity to the Illuminative cognition than is the particular. . .Since it is from the general or universal concepts that the largest deductive development is possible, it follows that a philosophy grounded on the Illuminative Cognition would elaborate itself mainly as a deductive system. . .Here we can see the possibility of a mathematic which is a revelation of truth."[55] In other worlds, since the abstract or universal is closer to Truth than the concrete or particular, it introduces the least distortion when used to symbolize or embody that truth; and since mathematics constitutes our most abstract language, it has the potential to carry the purest revelation of truth.
Although abstract concepts are excellent vehicles for carrying transcendent values, they are still, in themselves, objects in the relative world and can therefore never completely convey the non- relative content of transcendent states. "There is an irreducible incommensurability which forever makes correct cross-translation impossible. . .Still, there is such a thing as approximation to cross-translation in much the sense that a mathematician can give an approximate rational evaluation of an irrational number, such as the square root of 2."[56] To completely cross-translate the square root of 2 would mean to completely specify all the digits of its decimal expansion; but the decimal expansion of the square root of 2 has an infinite number of digits with no repeating pattern; thus to completely specify all the digits in its decimal expansion would require an infinite amount of time; it is therefore impossible to completely cross-translate the square root of 2 within the temporal bounds of the relative world. It is the same, Wolff says, with attempts to express the transcendent within the bounds of the relative world.
Nevertheless, even though we can never completely capture the irrational with the rational, we can obtain increasingly precise approximations by taking more digits in the expansion. Using abstract mathematical symbols to cross-translate transcendent states thus corresponds to a very precise approximation of an irrational number by a rational. Thus, using mathematical concepts, it is possible to express subtleties of transcendent states with much greater precision than with ordinary language. In one of his efforts at cross-translating, for example, Wolff says that "we are here dealing with a very profound conception where, again, it seems that only mathematics can help us."[57]
Wolff repeatedly uses mathematical symbols and metaphors where conventional language seems to fail completely. His most frequently used mathematical symbols are Infinity, Space, Point, and Zero. Infinity was most notably used in reference to the High Indifference. "Just as in mathematics there are infinitudes of higher orders infinitely transcending lower infinities, so it is in the Transcendent World. . .I have found an Infinite World, and then another Infinite consuming the first. . .It is an Infinity of some higher order, that is an INFINITY which comprehends lesser Infinities."[58] Here Wolff refers to Cantor's mathematical theory of transfinite numbers. In his famous diagonalization argument, Cantor proves that one transfinite number can be larger than another, in particular, that the number of points on the real number line between zero and one is greater than the number of positive integers. The proof begins by supposing that these two infinite numbers are equal, i.e. that the points on the number line can be put in one-to-one correspondence with the positive integers. If, as supposed, we can number each point with a positive integer, then we can make a sequential list of all the points, writing the decimal expansion of each real number next to its corresponding positive integer.
| 1 | 0.029384710... |
| 2 | 0.470128374... |
| 3 | 0.234928702... |
| 4 | 0.872938472... |
| 5 | 0.295629056... |
| 6 | etc. |
By supposition, this list completely enumerates every real number. Yet it is not complete since there are numbers not on the list. For example, construct a number that has its first digit different from the first digit of the first number, its second digit different from the second digit of the second number, its third digit different from the third digit of the third number, and so on. This will result in a number that differs from every number on the list and yet it specifies a point on the real number line. Therefore, the number of points on the real number line must be greater than the number of positive integers. Since both numbers are infinite, there are thus two infinities of different magnitudes. In fact, there are infinities beyond infinities in transfinite set theory. These infinities are just two of the smallest infinities.
Another aspect of the High Indifference is the Realization of two-fold egolessness, i.e. the relativity of both the personal and transcendental egos, both the self and the Self. To communicate this notion, Wolff uses the mathematical conception of a parameter. "With respect to a specific entity, the invariable identity is the Self, but with respect to all creatures and all modes of consciousness, the Self becomes a parameter that varies. Behind and supporting this parameter is the ultimate invariant, Pure Consciousness Itself."[59] The mathematical meaning of parameter to which Wolff refers is as follows. Take, for example, the equation x^2 + y^2 = r^2, which describes the set of points (x, y) in the plane that are at a constant distance r from the point (0, 0), i.e. a circle with radius r centered about the origin.
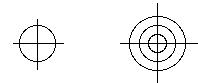
The description just given takes the variable r to be constant. For this fixed value of r, the equation yields a single circle through the variation of the values of x and y. Yet we may change the value of r to yield another circle having a different radius. Thus, through the variation of r the equation yields a whole family of circles. A variable like r which has a fixed value with respect to other variables is called a parameter. The Self, which is a relative invariant with respect to the rounds of cyclic existence, corresponds to the value of r, which is a relative invariant with respect to the values of x and y around the circle. Yet the value of r, like the Self, is only a relative invariant since it can change to yield different rounds of cyclic existence. The absolute invariant, which all the circles have in common, is their common centerpoint and the entire Space in which they reside.
Corresponding to twofold egolessness is a twofold emptiness or zero. On the one hand, Wolff uses zero as a symbol for the Self stripped of all objects. "Here we have a notion which stands for nothing, and yet becomes the most vital unifying conception of mathematics. . .Upon zero we build our systems of reference, which is merely a way of saying that with nothing as a center we have the fulcrum for control of all elaborations in form. . .The pure 'I' is the zero-point of organized consciousness."[60] This first egolessness, this bare point-I, is then transformed into the Space-I. "The Transcendent 'I' is as much a space as a point. Its mathematical symbol would be both 0 (zero) and oo (infinity)."[61] Yet in the High Indifference, this Self blows out leaving only Consciousness- Without-An-Object (and Without-A-Subject). "Consciousness-Without-An- Object is the universal solvent within which the centers of tension, or objects, have their field of play. All tendency in that play is counter-balanced by its counter-tendency, the culminating effect being an expression equated to zero. It is zero that symbolizes the durable Reality, or Consciousness-Without-An-Object."[62] This is the higher sense of zero or emptiness, symbolizing the cancellation of the positive and negative polarizations corresponding to the Universe and Nirvana.[63]
Wolff coined the term 'inverse cognitions' to describe cognitions polarized in the opposite sense as objective cognitions, i.e. toward the Nirvanic. "Awareness of the absence of objects, in its purity, is not a cognition of an object, but another form of consciousness that is not concerned with objects. However, a reflection of this state of consciousness may be produced so that a special cognition arises, of such a nature that its content is definable as the inverse of all objects. . .illustrated very well in mathematics in connection with the development of the notions of negative, imaginary, infinitesimal, and transfinite numbers. All these may be regarded as of the nature of inverse cognitions."[64] Since inverse cognitions are of a non-objective nature, they involve mystical recognition. Wolff also mentions the continuum as another inverse cognition, polarized opposite to the discrete nature of the Universe of objects. "It is true that man has arrived at the notion of continuity, although. . .he never really thinks it. . .Continuity belongs to the hinterland of Consciousness. This simply illustrates the eternal fact, i.e. that the actual consciousness of man continually operates in a Nirvanic as well as in a Sangsaric sense."[65] Thus these inverse cognitions found in mathematics are profound vehicles for recognizing the Nirvanic pole of consciousness.
The conceptions of negative, imaginary, infinitesimal, and transfinite numbers, as well as the conception of the continuum, are all symbols for inverse cognitions by virtue of their common transcendence of the conventional universe of positive integers. We have already seen how the infinity of the continuum transcends the infinity of positive integers with respect to the size of the infinities present in each type of number. The transcendence, however, is also a transcendence of the kind of number. It is a liberation not only from quantitative bounds, but also from qualitative bounds into new forms of number having more universal laws. For example, within the bounds of positive integers the laws of subtraction are limited by the requirement that the result must be positive. With the birth of the conception of negative number, however, no such limits need be imposed upon the laws of subtraction. Similarly, within the bounds of real numbers the laws for taking square roots must be restricted by the requirement that square roots may only be taken of positive numbers. With the birth of imaginary numbers, however, no such limits need be imposed. Similarly, in the case of transfinite and infinitesimal numbers the laws become less restrictive and more universal. What was impossible before is now possible. For example, a transfinite number can be divided in two without decreasing in size. These new forms of number thus symbolize a way of consciousness where the restrictive forms of our conventional universe are transcended, where the impossible becomes the possible, and where new forms of reality are realized where there was nothing before.
The latent Nirvanic powers of mathematical conceptions provide valuable symbols for the transformation of the mind. "It is possible to take the symbol itself as an object of thought and use it for the purposes of philosophical and general mystical integration. . .There is some reason to believe that such a method of procedure is possible within the setting of Western culture. . .This possibility I see as growing out of our peculiar mathematical development."[66] Moreover, "the greatest achievement of western genius has been in the development of the abstract thought which has its crown in higher mathematics. The freeing of thought from dependence upon the sensible image is an accomplishment of the very greatest difficulty. Until thought has won this power, it cannot penetrate into the Realm of Imageless Consciousness. Now, once it is realized how much has been accomplished in this direction in the field of higher mathematics, it is easy to see what a powerful instrument in the practice of Dhyana we have forged."[67] Because of its very abstract nature, mathematics can carry one to the utmost limit of subtle form where the leap to the Transcendent is relatively small. "The labor whereby a man attains the point of working with objects of highest tenuity actually implies much of the austerity requisite for the achievement of true objectlessness."[68] The activity of mathematics, thus is a powerful method for training the mind to be receptive to subtle forms and, consequently, formlessness. "In my own experience, thought on the level of Imageless Consciousness was possible by employing the intellectual capacities unfolded during the years of mathematical discipline."[69]
There are other equally important contributing factors to the transformation of the mind by mathematics. "The validity of mathematics is established upon a basis that is quite impersonal and universal. . .In its purity it deals only with transcendental or ideal objects of the very highest order of thinkable abstraction or universality. In high degree, the consciousness of the mathematician qua mathematician is not concerned with either a self or objects. . .in higher degree than anywhere else, except perhaps in states of samadhi of a high order. Herein is revealed the power of pure mathematics as an instrument of consciousness- transformation on a very lofty level."[70]
Here we begin to touch upon important aspects of the spiritual power of mathematics: its universality, impersonality, and selflessness. When we enter the realm of mathematics, we transcend the realm of the personal human and enter a realm of universals. "Man will have long since ceased to be human, in the restricting meaning of the term, by the time he has awakened in terms of Consciousness at the most advanced levels represented by mathematical concepts and symbolic formulae. Mathematics thus constitutes a thread to the Beyond that has never been lost."[71] Moreover, "for him who penetrates deeply into the roots of logic itself, the Recognition can be aroused. . .Let a man unveil this Recognition and make It immediately and consciously his own, and then he will find in logic a power which, if followed with a single eye, will take him through to the Higher Consciousness."[72] Furthermore, "pure mathematics is the only real invariant that we have in the ever- changing phantasmagoria of experience. . .the law that governs the flow of consequences [in a mathematical system] is tougher than tempered steel and harder than the hardest rock. Save in the Self, here, as nowhere else, is there something to which human consciousness may tie and give its trust. . .and this invulnerable core carries straight through to Consciousness-Without-An-Object."[73]
Mathematics is not only a thread by which we may know the Beyond, but also a means by which we may commune with it. Just as mathematics gives us deeper vision into the outer structures of the objective world, so "the 'eye' of the mathematician actually sees into the deep structure of the subjective psyche. . .May it not be that the mathematical thought is the speech of the Divinity in the inner consciousness of man? Then the mathematical thought is inner communion."[74] Here we begin to see a glimmer of the heart and soul of mathematics. "Without the Recognition of Soul, in some sense, such as the soul of mathematics or of logic or in some other form, formal demonstration proves merely possibility or the hypothetical imperative but never arrives at the categorical imperative. The only knowledge that can possibly Liberate man is categorical."[75]
Thus the transformative power of mathematics lies not only in its form and logic, but also in its soul where it is felt with the heart. Indeed, Wolff points out, in regard to the use of mathematical symbols for spiritual transformation, that "to step from the symbol to that which is symbolized, though this does afford a peculiarly exacting demand upon acuity of thought, yet requires much more. Here, feeling, in the best sense, must fuse with thought. The thinker must learn also to feel his thought, so that, in the highest degree, he thinks devotedly. It is not enough to think clearly, if the thinker stands aloof, not giving himself with his thought. The thinker arrives by surrendering himself to Truth, claiming for himself no rights save those that Truth herself bestows upon him. In the final state of perfection, he possesses no longer opinions of his own nor any private preference. Then Truth possesses him, not he, Truth. He who would become one with the Eternal must first learn to be humble. He must offer, upon the sacrificial alter, the pride of the knower. He must become one who lays no possessive claim to knowledge or wisdom. This is the state of the mystic ignorance -- of the emptied heart."[76]
Thus the transformation of the heart is an essential part of the method which employs mathematics for spiritual realization. Mathematics can itself aid in this heart transformation by virtue of its embodiment of Truth in a particularly pure form. Mathematics thus provides an excellent object of devotion. This played an important role on Wolff's path. "A desire for the transcendent Self and a love of universals also tend toward the required melting of the egoistic feeling. In this part of the discipline I found that my already established love of mathematics and philosophy was an aid of radical importance."[77] Indeed, "in the cognitive activity of pure mathematics. . .the desire is almost wholly directed toward Truth and Beauty, with little or no attachment to any preconception of what Truth may ultimately prove to be. Cognitive activity of this type. . .may well prove to be one of the most powerful subsidiary aids for those who can make use of it."[78]
The essential key to employing mathematics as a transformative discipline, then, lies in the heart we put into it. "The two great factors which implement the motivation underlying the drive toward Mystical Realization are (1) Love of Truth, and (2) Compassion. . .Compassion and the Love of Truth are the only valid and effective motivations, and the Compassion must be utterly self-disregarding, and the seeking of Truth must be so pure that every preconception is offered up on the alter of sacrifice."[79] Thus, "one can raise a study to the status of an effective transforming agent only by giving himself to it with the same completeness that is characteristic of the more intense religious natures. . .It is just the subtle change implied in the difference between secular and sacred which makes all the difference in the world. In principle, anything whatsoever can acquire the sacred value; it is simply important that the attitude of sacredness shall exist and shall absorb the predominant portion of the interest. Sacredness implies self-giving, while secularity implies self- withholding. In the transformative process, everything else is incidental to the attaining of the self-giving attitude."[80]
Thus mathematics, when practiced with great devotion and humility, necessarily involves the transformation of both mind and heart and leads inevitably to both Compassion and Wisdom. It is one path, albeit not for many, which combines logic with love and conception with compassion.