share

Mathematics: The Bridge to an Integral Science of Experience

Through a reflection on the nature of mathematics, the author proposes a modified scientific method that includes inner experience and discusses its implications for the scientific study of consciousness.

The scientific method is generally thought to require that scientific verification draw only from outer experience, thus excluding all inner experience as a valid basis for scientific verification. Consequently, the scientific study of consciousness today is largely limited to the physical sciences and the externally observable correlates of consciousness. Mathematics, however, provides an example of a rigorous science based on inner experience that is nonetheless verifiable. Contrary to widespread belief, it is possible, therefore, for an authentic science to be based upon inner experience.

The author then suggests how a science of consciousness can be based on inner experience. Significantly, such an "inner science" of consciousness (as opposed to the conventional "outer science" of consciousness based on external observation) is not limited to studying the physical correlates of consciousness, but includes inner conscious experience itself. The "hard problem" of consciousness, therefore, is only "hard" for outer science of consciousness because it excludes inner experience from its domain.

This science of inner experience is then generalized to a science encompassing both inner and outer experience. This generalized scientific framework, which the author calls Integral Science, contains as special cases the well-known physical sciences of outer experience as well as the less obvious sciences of inner experience, such as mathematics and an inner science of consciousness. The apparently conflicting approaches to the study of consciousness--those based on inner experience and those based on outer experience--can be viewed from the framework of Integral Science as complementary ways of investigating consciousness from different perspectives, each of which alone is incomplete.

There is no such thing as knowledge apart from, or outside of, our experience. Thus, all scientific knowledge is fundamentally grounded in our experience. All science, therefore, is the inquiry into the nature of our experience constrained by the essential principles of the scientific method. In particular, a genuine science of consciousness must take experience itself as its ground.

If we forget that our scientific knowledge is ultimately derived from experience, then the physical world appears to be an objective reality separate from our experience. As a result, we are confronted with the "hard" problem of how physical reality gives rise to experience. The solution to this problem is not to devise a more sophisticated model of physical reality, but to recognize that our question is based on a false assumption.

Grounding science in just external experience, however, is not enough. Science limited to external experience is like a person who looks only at objects and shadows and refuses to look at light and the sun. Just as such a person will never explain how light is related to shadows, a science limited to external experience will never explain how inner experience is related to outer experience. Consequently, any theory relating inner experience to external correlates of consciousness will be unverifiable. (Note that there is a subtle but important distinction between inner experiences themselves and external correlates of inner experiences, such as verbal reports, behavior, brain scans, physiological measurements, etc.)

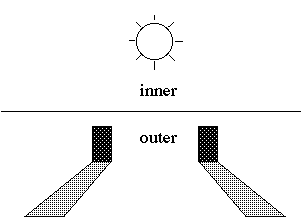
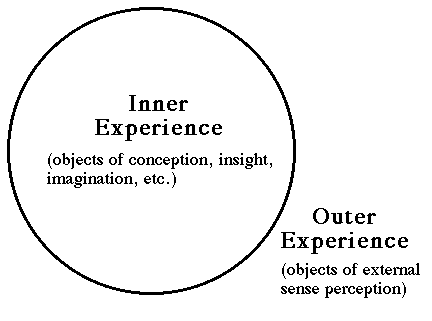
We commonly regard our experience as divided into two domains: the inner domain of experience and the outer domain of experience.

Outer Domain

The outer domain of experience includes what we normally regard as our experience of the external world. We experience the outer domain through our sensory faculties of apprehension, i.e., vision, hearing, touch, taste, and smell. We typically regard objects of outer experience as other than our selves, thereby distinguishing them from objects of inner experience, which are within or part of our selves.

Inner Domain

The inner domain of experience includes our experience of objects inside ourselves, such as the inner world that we experience through our inner faculties of apprehension. These inner faculties include, among other possibilities, conception, imagination, and insight. Examples of inner objects of experience are concepts such as mathematical equations and philosophical propositions, affective states such as joy and fear, and various subtle states of consciousness.

It is conventional to divide knowledge into two broad classes: public or interpersonal knowledge, and private or personal knowledge.

Public Knowledge

Knowledge that is public or interpersonal is knowledge that is shared, or agreed upon, by a community of individuals. For example, we all agree that there is a floor here beneath us. Physicists agree with each other on the charge of the electron. Mathematicians agree with each other that the Pythagorean theorem is true. Note that public knowledge is relative to a specific community of people and is associated with generally accepted methods and procedures for verifying the validity of their shared knowledge, thereby distinguishing it from private or personal knowledge.

Private Knowledge

Private or personal knowledge is knowledge that is idiosyncratic and specific to individuals. For example, our dreams and fantasies are not usually accessible to each other. While I can know with certainty that I had a dream about an elephant stampede last night, there is no way you can verify or falsify this claim. Consequently, my dream is not considered shared knowledge.

The distinction between inner and outer experience is different from the distinction between private and public knowledge. Inner experience can be public. For example, mathematical knowledge is public ("objective"), and yet it is based upon inner ("subjective") conceptual experience within the minds of mathematicians. Although theorems in mathematics may be communicated via outer experience, they are not verified or falsified in outer experience, but by appeal to inner experience. Thus, mathematics demonstrates that there are regions of inner experience that can form the basis for public knowledge.

The public nature of scientific knowledge derives not from the fact that its data is collected from the external world, but from the fact that the method of verification includes conditions which have been made explicit, communicable, and reproducible by others. Thus, another observer who understands and properly generates the same conditions can have largely the same experience. The distinction between public and private knowledge, therefore, is that the former is characterized by common conditions of observation, while the later is not. Science can then be understood as a process of becoming aware of and reproducing the conditions of our observations. Because this process operates in both inner experience and outer experience, the distinction between inner and outer is not the same as the distinction between public and private.

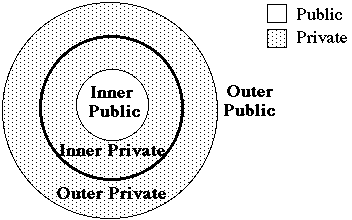
Since the distinction between private and public does not coincide with the distinction between inner and outer experience, we can divide our experience into four regions as shown in the table below.

	Private Knowledge	Public Knowledge
Outer Experience	Private Sensory Experience	Outer Public Experience
Inner Experience	Private Conceptual and Affective Experience	Inner Public Experience

Accurately discerning the distinction between public and private, can be a difficult task. Learning to properly make this distinction in practice is of central importance in any science. In fact, learning to make this distinction is the basis for our common consensus reality, and we can view science as a refinement of our learned ability to make this distinction.

We can confuse the public/private distinction with the inner/outer distinction, however, because such a large portion of our attention is focused either in outer-public experience or inner-private experience, and we easily ignore outer-private experience and inner-public experience. We are then left with the mistaken impression that inner experience is necessarily private and opposed to outer experience which is public.

We can now augment our original map of experience to reflect the types of knowledge within the inner and outer domains:

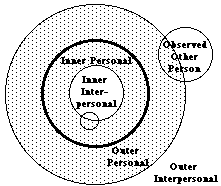
Ring of Private Knowledge

In this symbolic representation of experience, our private or personal knowledge corresponds to a ring of experience. The distinction between inner and outer divides this ring into a ring of inner personal knowledge and a ring of outer personal knowledge. The former contains our private knowledge of our inner feelings, thoughts, and so on. The latter contains our private knowledge of the sensory world, e.g., what we see from our point of view, what we can hear in this part of the room.

Inner and Outer Regions of Interpersonal Experience

The impersonal region is the complement of the personal ring of experience, and it consists of an outer impersonal portion and an inner impersonal portion. The outer portion contains that part of outer experience that is considered interpersonal or shared, and it is the task of Outer Sciences, such as physics, to explore this region and determine its nature and laws, i.e. those aspects that can be abstracted from our shared experience. Similarly, the inner portion contains that part of inner experience that is impersonal or shared. Inner Sciences, such as mathematics, explore the nature and laws of this region. Mathematical truths, for example, are structures of inner conceptual experience that are invariant from person to person. Certain very deep psychological structures might also be considered public structures of inner experience (e.g., Jung's archetypes of the collective unconscious, Kant's categories of the understanding and forms of the sensibility.)

Because mathematics is a living example of a well-developed inner science, it has many things to teach us about how to properly extend science into the realm of inner experience. In addition, using mathematics as a prototype of an inner science and physics as the prototype of an empirical science, the notion of science and the scientific method may be generalized so that it is comprehensive of both inner and outer domains of experience. Because such a generalization of science integrates both inner sciences and outer sciences into one generalized science that is comprehensive of both, I have called it integral science (McFarlane, 1996) so as to distinguish it from the more restrictive special case of empirical science. Ken Wilber (1979, 1990) and Charles Tart (1972) have also made proposals for an epistemological extension of science to include more than our ordinary sensory experience of the world. This presentation focuses on the special role that mathematics can play in such an extension.

Verification in Outer Science and in Inner Science

It is a fundamental principle of Outer Science that hypotheses be subjected to verification in the outer domain of experience by a community of trained practitioners. A physical theory, for example, is subject to the condition that its predictions must be compatible with our sensory experiences of the world of outer objects. It is important to note that only trained physicists are qualified to test physical theories against experience.

Similarly, it is also a fundamental principle of Inner Science that hypotheses be subjected to verification by a community of trained practitioners. A mathematical theorem, for example, is subject to the condition that its proof must be compatible with our inner conceptual experiences, in particular, the inner experiences of trained mathematicians. Note that the method a mathematician uses to verify a proof of a theorem does not require or depend on any external empirical data but rather appeals to an inner examination in the mind. The theorem that the number of prime numbers is not finite, for example, is a mathematical truth that cannot be proved or disproved by appeal to our external experience. Yet, this truth is verifiable and is public knowledge, clearly demonstrating that certain aspects of inner experience can be just as public as aspects of outer experience.

From the above, we form a generalized principle of verification which does not depend on the domain of experience: Propositions are subject to verification in experience (i.e., in the inner and/or outer domains of experience) by a community of trained practitioners. In the case of Outer Science, verification is grounded in our outer sensory experience. In the case of Inner Science, verification is grounded in our inner experience. Insofar as the inner and outer domains of experience are merely two aspects (and arguably arbitrary ones at that) of a coherent and integrated ground of all experience, we may simply say that Integral Science is simply the science of experience, both inner and outer. It has no bias, therefore, toward either subjective idealism or objective realism, but operates in an experiential context comprehensive of both the inner and outer domains.

The Outer Science of Inner Phenomena

Although the methods of Outer Science can be applied to outer manifestations that we may attribute to inner phenomena, Outer Science can not study inner phenomena directly. For example, the methods of outer science can be used to externally study the brain, the behavior of people, and even verbal reports of their inner states. But we can never gain direct access to the inner states of other people through our faculties of outer sensation. Indeed, since Outer Science is limited to the faculties of outer sensation, it can not even establish with certainty that other people even have inner states at all. Trying to verify a proposition about inner states of consciousness by looking at brains and behavior in the external world is like trying to prove a mathematical theorem to yourself by studying the behavior of other mathematicians.

The Inner Science of Inner Phenomena

Just as the best way to study outer phenomena is to directly observe them in the external world, the best way to study inner phenomena is to observe them directly in the inner world. The challenge is to develop the subtle concepts and discernment necessary to properly distinguish between the personal and impersonal components of inner experience. For example, just as in outer experience the scientist needs to carefully distinguish personal "subjective" biases from so-called "objective" attributes, one must do the same with inner experience. Verification within a community of practitioners is one technique for helping mitigate bias in both outer and inner sciences.

The Scientific Method in Inner and Outer Experience

	Outer Science	Inner Science
Prerequisite Scientific Training	Develop an understanding of astronomy, obtain a working telescope and an ability to properly operate it	Develop an understanding of arithmetic and logic, obtain a mind capable of clear and correct conceptual thought
Experiential Observation: Isolate a portion of experience for careful observation	Point the telescope steadily at Jupiter over the course of several clear nights and record the positions of luminous objects near Jupiter	Direct attention steadily over the course of several days upon the question of whether there are a finite number of prime numbers, and record insights into the problem
Theoretical Analysis	Analyze the data collected based on your understanding of astronomy, taking into account any biases or errors that may have been introduced in the observation	Analyze the insights based on your understanding of mathematics, taking into account any errors of logic or misconceptions introduced in the investigation
Propose a Hypothesis and Report your results to Others	Propose a hypothesis that Juptier has moons, and communicate your hypothesis, your data, your method of collecting the data, and your reasoning that the hypothesis is consistent with the data	Propose a theorem that the number of primes is not infinite, and communicate your theorem, your reasoning leading to the insight, and your reasoning that the theorem is consistent with the insight
Independent Verification by other trained practitioners	Based on your reports, other trained astronomers attempt to replicate your external observations and verify or falsify your hypothesis	Based on your reports, other trained mathematicians attempt to replicate your insight and verify or falisfy your theorem

The Unreasonable Effectiveness of Mathematics

It seemed remarkable to Eugene Wigner, and to many other people as well, that our mathematical structures, these "free creation of the human mind" as Einstein called them, should correspond so perfectly to the structures found in nature. It seems quite miraculous at times, and most explanations just do not seem entirely satisfying.

There appears to be a deep connection, if not identity, between our inner psychological structures and the structures of the outer world of experience. Although the inner and outer interpersonal regions appear disconnected, they may actually be intimately related to each other. When we look into the outside world we often are looking at a world colored by projections of our personal unconscious contents. Perhaps projections of our collective inner consciousness gives rise in a similar way to our collective outer world. This hypothesis makes it very reasonable that there be an effectiveness of mathematics in physical science: When we look within ourselves to mathematical structures, we are exploring the very forms that give structure to our outer experience. Similarly, the other universal structures within us, such as Jung's archetypes, correspond to the outer structures we experience in the external world as objective.

These inner forms are not of a personal nature and are not subject to manipulation by our personal will. We can no more change these structures of experience with our personal will than we can change the laws of mathematics by wishing them otherwise.

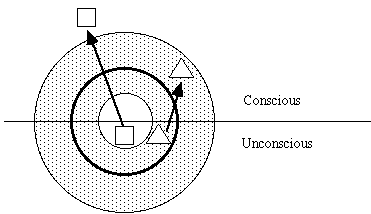
The process of psychological projection depends on a breaking of the integrated field of experience into two parts, an unconscious part and a conscious part. The conscious fragment of any structure is the projection or reflection of its unconscious complement. Kant's Categories of the Understanding and Forms of the Sensibility are inner structures projected outward as objective structures of space, time, causality, and so on.

Levels of Law and Invariants of Experience

This model implies a hierarchy of experience: deeper structures of inner experience correspond to more and more universal or invariant forms, while more superficial structures in the personal sphere correspond to structures that are less invariant and more contingent. These structures are then projected out to give their mirror in the outer world of experience.

Our perceptions of the physical world are highly individualized. Two people looking at a table, for example, see it from different physical perspectives and have visual perceptions of the table that can be very different. The view straight on from the side is very different from the view from above. If these two people were limited to their different perspectives of the table, they would be unable to correlate their experiences with each other and abstract the notion of a public table. It is only through their ability to change their perspectives, abstract conceptual models of the various perceptions from the different perspectives, and communicate them to each other, that they can understand their otherwise private experience to have a public component. If their experience remains limited to one perspective, they will be unable to come to this understanding, and they will consider their experiences of the table to be private. This suggests the possibility that much of what we presently consider to be strictly private experience can, with the further development of science, be understood as our particular perspective on a shared public experience. Such a development, however, requires an exploration of the different possible perspectives on our experiences, and freeing ourselves from limited domains of experience. One of the important lessons of relativity theory and quantum mechanics is that we must take proper consideratin of our perspective or frame of reference when making observations (Bohr, 1935). As will become evident from the discussion below, this lesson is also important when making inner observations.

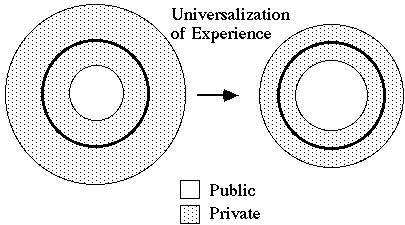
All science has progressed by developing increasingly subtle and refined methods of discerning public aspects of experiences. By subjecting our experiences to intersubjective agreement, we learn to isolate and abstract from these private experiences the universal aspects that are independent of the observer. In mathematics, for example, we are trained to discriminate between inferences that conform with the canons of logic and those that do not, and we learn to understand subtle relationships between mathematical objects. It takes considerable time contemplating the Lebesgue theory of integration, for example, to fully understand which mathematical functions can be integrated and which cannot. Through this mental training, we learn to clearly discern the universal elements of public experience that every mathematician shares. The ability to reliably develop this power of discernment, however, must be cultivated and developed over years of mental training.

An important first step in the process of discriminating public features of experience is to identify and isolate some of the simple salient features and work with them, while ignoring (for the time being) the rest of the complexity of experience. Because it is never obvious at first what the appropriate features are, or how to identify them, one usually studies under the guidance of someone with more experience. Without such guidance, it takes creative genius to identify and abstract useful features of experience. For example, it took the genius of a Galileo to abstract the idea of frictionless motion from a world full of friction in all its complexity. Elementary physics is simple because it starts with simple models based on observations that ignored a lot of the complexity. Then, through refinement over centuries, the theory and observations both become more and more complex and subtle. Today, observing a top quark is an exceedingly complex task involving hundreds of people working for months with a particle accelerator, then applying the esoteric theories of elementary particles to interpret the data and arrive at a conclusion about what was measured. Similarly, it took the genius of the ancient Greeks to identify the abstract notion of a deductive mathematical proof and to isolate the axioms of geometry. Through subsequent refinement over the centuries, however, mathematics today is exceedingly more complex and subtle. To even come close to understanding the frontiers of research in algebraic topology, for example, requires several years of mathematical study at the graduate level. Yet, both mathematics and physics have started with isolating some of the simplest structures and progressively refining them over the centuries. The complexity of experience, therefore, need not be taken into account entirely at the beginning of a science, or our study of it. In particular, one expects that a successful first step in the development of an inner science of consciousness would involve isolating certain sailient features of inner experience and ignoring most of the complexity. The complexity would gradually be taken into account only later as the science evolves.

One of the difficulties in any science is distinguishing an experimental error from genuine data during an attempt to verify a claim. If we fail to see moons moving around Jupiter, for example, it might be that we have mistaken a bright star for Jupiter, or we have a poor telescope without sufficient power and resolution to clearly see the moons. The weather may be bad, or Jupiter may not be visible at all during the night from our position on Earth that season. We may have recorded the positions of the moons incorrectly or we may have inadvertently changed the magnification power of the telescope from night to night. Thus, verifying the claim may require that many very specific conditions be satisfied. So, if someone fails to verify a scientific claim, it may be due to the fact that all the experimental conditions were not satisfied, rather than due to the claim being false. It is just the same with inner verifications of mathematical theorems. If we fail to verify that there are an infinite number of primes, for example, it may be due to any number of problems with our attempt to verify the theorem. We may not have a clear proof to follow, or it may not be complete. We may have a distracted mind that is unable to clearly focus on the steps of the proof and see how they logically relate to each other. We may not understand certain concepts used in the proof, or we may have simply made a logical mistake. Any number of other problems may have prevented us from verifying the proof. So our failure to verify a scientific claim may often be evidence of our inability to apply the method of verification rather than evidence that the claim is false or unverifiable. Although obvious in the physical sciences, this can be easily overlooked in the case of an inner science.

Because every scientific verification depends upon the satisfaction of numerous specific conditions, the use of controlled experiments to verify knowledge is an essential component of science. Although it begins with ordinary experience, the power of modern science derives not from ordinary experience, but from extraordinary experience which has been contrived by subjecting experience to specific conditions in a laboratory. This principle is the same in a science of outer experience, such as physics, as for a science of inner experience, such as mathematics. We would not have any of the profound insights of modern physics without experimentally probing the world in very specific and non-ordinary ways that make use of particle accelerators and other elaborate instruments. Similarly, to verify Andrew Weil's recent proof of Fermat's Last Theorem[1] requires a very non-ordinary inner instrument, namely, a mind trained to discern very abstract and refined mathematical objects that are not accessible to the mind of an average person. We should expect that an inner science of consciousness, like other sciences, should look to extraordinary experience rather than to ordinary experience.

In the case of empirical science it is well understood that the verification of scientific claims requires not only elaborate experimental devices but also considerable skill and training on the part of the scientist. Thus, a scientific claim is not normally verifiable except by individuals who first undergo the prerequisite training in a specific scientific field. Only a trained astronomer, for example, is able to reliably test a claim that a distant star has a planet orbiting it. Similarly, only a trained mathematician is able to reliably test a claim that Fermat's Last Theorem is true. Depending on the degree of development of the science, the requisite training may involve years of education followed by many more years of advanced training in both theoretical and experimental techniques. Whether the claim be one of inner science or outer science, only a trained specialist is qualified to reliably test scientific claims. Others who attempt such tests will most probably fail to verify the claim, demonstrating not that the claim is false but that they lack sufficient training to successfully verify it. In particular, a genuine scientist cannot justifiably dismiss experiential claims by others who are trained in the theoretical and experimental methods of a particular science of experience, whether it be inner experience or outer experience, unless the scientist has also been similarly trained.

The extensive training of a scientist develops the skills necessary to successfully verify scientific claims. In addition, independent verification by other trained scientists in a community plays an important role in science since it helps prevent the confusion of experimental errors or other particular phenomena of a non-universal nature with actual verifications or falisfications of a public nature. Thus, scientific traditions rely upon a group of trained peers to test their personal experiences. For example, the proof of Fermat's last theorem by Andrew Wiles began as a personal insight in his consciousness. It was not officially accepted by the mathematical community until it was validated by a group of qualified peers. This peer review checks the experience or experiment using the methods of verification known within the particular specialty.

In order to allow an experiment or experience to be tested by peers, it is necessary that the method of validation is communicable. This communication, however, need not be comprehensible to scientists outside the special field of inquiry. A proof of a theorem in algebraic number theory, for example, is just as incomprehensible to the typical physicist as an experimental procedure involving the operation of high energy particle accelerator is to a typical mathematician. An experimental method of verification, therefore, whether directed toward an inner experience or an outer experience, requires that the description of the verification procedure be comprehensible to scientists trained in the specific field of concern. The more developed a scientific field, the more likely its methods of verification will be incomprehensible to those outside the field. Although all scientists should be encouraged to communicate their methods as clearly and simply as possible, they should also be aware that methods of verification are not necessarily invalid simply because they are not comprehensible to non-specialists.

In addition to the methods of verification, the descriptions of the resulting experiences and the truth claims are also not necessarily comprehensible to non-specialists. In particular, only trained specialists are able to properly interpret and confirm experiences resulting from verification procedures, and understand knowledge claims that they relate to. For example, most theorems in advanced mathematics will not be comprehensible to the typical novice, and only the specialist will understand them. Similarly, Einstein's equations of general relativity are not comprehensible to novices, and only specialists with years of training can understand them. Science, therefore, requires only that descriptions of knowledge claims and experiences be understandable among a group of scientific peers. In other words, the communication of scientific knowledge, whether inner or outer, requires specialized scientific training. In particular, the failure to communicate inner experiences or knowledge claims may well be due to an insufficient training of the person trying to understand what is being communicated.

In both inner and outer science, the methods of verification are communicated as injuctions or instructions. In the case of outer science, these instructions usually pertain to the operation of an experimental apparatus in a laboratory. As we have noted above, however, these instructions also contain an implicit injunction to first become a skilled practitioner of the specific science within which the verification is taking place. Following this injunction requires the scientist to learn experimental skills and to master theoretical concepts. In short, it requires the scientist to undergo an personal preparation prior to performing the outer experiment. In the case of inner sciences, there is also an implicit injunction that requires the scientist to undergo personal preparation and training. The instructions for the experiment itself, however, pertain to an inner experiment rather than an outer one. Thus, the mind of the scientist is the laboratory, and various cognitive skills serve as the experimental apparatus. The mathematician, for example, directs attention inward and uses conceptual insights to follow the injunctive steps of a proof. Because the experiment takes place within the mind and relies upon 'in-sight' rather than 'out-sight', it naturally demands more preparation and training from the scientist. Just as the physicist requires good outer instruments in order to clearly observe outer phenomena, so the mathematician requires good inner instruments in order to clearly observe inner phenomena. The mind of the inner scientist, therefore, must be doubly trained. Not only must it be trained in the theoretical concepts and experimental procedures, but it also must be trained to serve reliably as the very instrument by which the experiment takes place. The development of inner sciences, therefore, impies the inner development of the scientists themselves. The fact that inner exploration requires inner transformation, of course, has been known for centuries in the contemplative traditions of the world.

In addition to mathematical objects, there are other aspects of inner experience that are public, and may be studied by inner sciences. The most profound and systematic investigations of these intersubjective aspects of inner experience have been developed within the contemplative traditions of the world. These traditions have not only developed conceptual frameworks for understanding public aspects of inner experience, they have also developed remarkably uniform techniques and disciplines for investigating inner experience. For example, techniques of meditation and contemplation have been developed with the specific purpose of cultivating experiences of specific nonordinary states of consciousness. These extraordinary states of consciousness are characterized by a high degree of simplicity, and are contrasted with the relatively complex states of ordinary consciousness. In ordinary states of consciousness, the subtleties of inner states are difficult to observe, just as the subtle features of outer experience (e.g. superconductivity) require extraordinary experimental conditions to observe. In refined states of consciousness, on the other hand, the subtle features of inner experience are more apparent. In other words, refined states of consciousness in inner science serve the same purpose as controlled experiments in outer science. They reveal and isolate aspects of experience that could not otherwise have been observed. In short, a subtle mind is required to observe subtle metal objects. Or, as Plotinus writes in his Enneads, "Knowing demands the organ fitted to the object."

In addition to controlled experiments, other features characteristic of a science can also be found in contemplative traditions. For example, these traditions also have layers of doctrines which correspond to layers of mastery in understanding and experience. Elementary teachings take their departure from common experience, while more profound teachings presuppose a deep understanding and extensive experience. A similar layering of doctrine in found in empirical science. For example, elementary physics teaches Newtonian mechanics, while advanced quantum physics and relativity presuppose a mastery of these fundamentals. It is also worth pointing out that Newtonian mechanics is still taught to beginning students even though it is now known to be inadequate to explain phenomena at atomic scales and at high velocities. These levels of theory function as successive stepping stones to more subtle and comprehensive understanding. Similarly, the contemplative traditions also have levels of teachings. In Buddhism this classification is perhaps made most explicit in the distinction between relative or conventional teachings and ultimate teachings.

The contemplative traditions are characterized by the cultivation of an inner form of knowledge that is non-conceptual. The possibility of developing and refining valid non-conceptual inner knowledge has long been recognized by contemplatives, both East and West. Plato, for example, compares this capacity to a physical organ when he writes in the Republic that "there is an eye of the soul which...is more precious far than ten thousand bodily eyes, for by it alone is truth seen." More recently, the 20th century Western philosopher Franklin Merrell-Wolff (Wolff, 1944, 1973, 1995) has provided a detailed first-person account and philosophical analysis of the activation of non-conceptual inner knowledge. In particularly systematic and rigorous Eastern contemplative traditions such as Tibetan Buddhism, this type of knowledge has been cultivated and subjected to centuries of exhaustive philosophical scrutiny and refinement. In addition, over the course of many centuries these traditions have developed sophisticated and very precise techniques and methods of developing non-conceptual insights, e.g., forms of meditative or contemplative practice, which permit trained pracitioners to reliably verify specific knowledge claims within the tradition (Wallace, 1996, 1998). These methods of inner experimentation are coupled with theoretical and conceptual systems which are used to guide and organize experience, just as they do in empirical science.

Thus, although their methods of verification are directed toward inner experience rather than outer experience, contemplatives nevertheless make knowledge claims that others who have extensive training in the theory and practice of contemplative investigation are able to independently verify. Although their methods may be unfamiliar and even incomprehensible to us, we should be careful not to dismiss such sciences out of our own ignorance of them. If we are to honestly test their knowledge claims as scientists, we must first undergo the training ourselves which enables us to become capable practitioners. Otherwise we are no better than the dogmatists who, trapped within the artifical limits of their own world view, refused to even look through Galileo's telescope. Will the institution of emprical science suffer a similar fate as these dogmatists, or open itself to the inner knowledge developed by the contemplatives?

Because mathematics is itself a well-developed inner science and already has deeply established connections with empirical science, it is very possible that mathematics can serve as an important bridge between outer empirical science and inner contemplative sciences. In addition to the methodological lessons it can teach us about inner sciences in general, there are two important ways in which mathematics may function in the context of an inner science of consciousness. First, mathematics can provide a language in which subtle inner phenomena can be represented or expressed, just as it provides a language in which subtle outer phenomena can be described. Second, mathematics can actually be used as a method or technique for inducing subtle inner states of consciousness. This second function, which results from the fact that the mind in inner science is both the instrument and object of observation, is unlike any function mathematics serves in the context of empirical science.

The possibility that mathematics may be used as a language for metaphysics has been suggested in the 20th century by Wolff (1944, 1973) and mathematician Rudy Rucker (1983). In the 19th century mathematician Georg Cantor (1883) considered mathematics to be a method for expressing metaphysical truths of infinity, as did theologian Nicholas of Cusa in his De Docta Ignorantia several centuries earlier. There is a precedent, therefore, for the application of mathematics as a language of inner science.

One of the reasons why mathematics is useful in physical science is that it is able to precisely represent structures and concepts that are far too subtle and refined for ordinary language. Because many inner experiences have a high degree of subtlty, it would not be surprising if mathematics were a useful language for inner science as well as outer science. In addition, mathematics has the virtue of being a very universal language. Wolff suggested that this is one important reason to expect that mathematics should be useful in expressing knowledge derived from subtle non-conceptual cognitions:

"The universal. . .is in closer affinity to the Illuminative cognition than is the particular. . .Since it is from the general or universal concepts that the largest deductive development is possible, it follows that a philosophy grounded on the Illuminative Cognition would elaborate itself mainly as a deductive system. . .Here we can see the possibility of a mathematic which is a revelation of truth." (Wolff, 1995)

Mathematics, then, can reveal or translate the subtle, or "higher", conscious experiences into a precise language, although this translation can never be perfect or complete. As Wolff puts it:

"The immediate content of the Higher Consciousness cannot be cross-translated, "but certain formal properties can be through the use of systematic symbols. . .In fact, if the consciousness-equivalents of the entities and operations of pure mathematics were realized, we would find that, in that great science and art, cross-translation in a lofty sense already exists." (Wolff, 1994)

Mathematics, in other words, already contains the formal language to express many of the subtle structures of inner experience--we need only discover the exact correlations between them, the mathematical correlates of conscious experience. In this connection it is interesting to note the remarkable fact that many constructs of pure mathematics were discovered decades or centuries before it was realized that they exactly describe certain outer phenomena (Wigner, 1960). The same may be true, therefore, of inner phenomena.

An important first step toward correlating mathematical structures with inner structures was taken by the mathematician G. Spencer-Brown (1969). He demonstrated how the mathematical structure of logical thought flows naturally out of the nature of distinction. In addition, Jefferey James (1993) has shown how an arithmetic of rational numbers can be based on the concept of distinction, thus making an essential connection with empirical science. The connection between distinction and inner experience derives from the recognition that distinction is implicitly present as a fundamental structure at the basis of all our experience. The contemplative philosopher Ibn Arabi expressed this insight in perhaps the most simple and direct terms: "The root of all things is difference." Our experience of separate objects, for example, presupposes spatial distinctions, and our experience of past, present, and future presupposes temporal distinctions. Thus the very stage upon which our experience of the world is played out is built upon implicit distinctions. Our inner experience of language and thought also presupposes distinctions. Any word or concept, insofar as it has any meaning at all, indicates a distinction between what it refers to and what it does not refer to. Thus, all manifestations within experience, insofar as they may be consistently conceived at all, are structured by the form of distinction. The mathematics of distinction, therefore, can provide a fundamental descriptive language that may be useful for a science of inner and outer experience.

In addition to its capacity to describe inner experience, mathematics may also provide techniques for inducing specific subtle states or phenomena. As Nicholas of Cusa wrote in De Docta Ignorantia, "Since there is no other approach to a knowledge of things divine than that of symbols, we cannot do better than use mathematical signs on account of their indestructible certitude." In ancient times Proclus, Plato, and Pythagoras viewed mathematics as discipline practiced in the service of contemplative knowledge rather than as a tool for use in the service of empirical knowledge. Wolff, however, provides perhaps the most detailed discussion of the use of mathematics for inducing subtle states of inner experience. According to Wolff, contemplation of the mathematical notions of negative, imaginary, infinitesimal, and transfinite numbers involves not only conceptual knowledge but 'inverse cognitions' that are non-conceptual in nature (Wolff, 1973). Wolff also identifies the mathematical continuum as another example (Wolff, 1973), and gives special importance to the notion of infinity (Wolff, 1944). These mathematical ideas, therefore, can be used as symbols to assist the contemplative in developing non-conceptual insights. As Wolff explains,

"It is possible to take the symbol itself as an object of thought and use it for the purposes of philosophical and general mystical integration. . .There is some reason to believe that such a method of procedure is possible within the setting of Western culture. . .This possibility I see as growing out of our peculiar mathematical development." (Wolff, 1973)

This type of practice is of service to the contemplative, he explains, because

"the greatest achievement of western genius has been in the development of the abstract thought which has its crown in higher mathematics. The freeing of thought from dependence upon the sensible image is an accomplishment of the very greatest difficulty. Until thought has won this power, it cannot penetrate into the Realm of Imageless Consciousness. Now, once it is realized how much has been accomplished in this direction in the field of higher mathematics, it is easy to see what a powerful instrument in the practice of Dhyana we have forged." (Wolff, 1944)

Wolff testifies that mathematics used in this way was a powerful method for training his own mind to be receptive to subtle forms of consciousness:

"In my own experience, thought on the level of Imageless Consciousness was possible by employing the intellectual capacities unfolded during the years of mathematical discipline." (Wolff, 1944)

Mathematics, therefore, can be much more than a conceptual framework with applications to outer experience. It can also be the very instrument for investigating subtle inner experience.

Wolff also testifies that the discipline of mathematics helps to purify the mind because

"in the cognitive activity of pure mathematics. . .the desire is almost wholly directed toward Truth and Beauty, with little or no attachment to any preconception of what Truth may ultimately prove to be. Cognitive activity of this type. . .may well prove to be one of the most powerful subsidiary aids for those who can make use of it." (Wolff, 1944)

This purification of the mind, which is analogous to the cleaning and fine-adjustment of Galileo's telescope, is directly related to the capacity to clearly observe inner experience. As Wolff goes on to explain,

"The validity of mathematics is established upon a basis that is quite impersonal and universal. . .In its purity it deals only with transcendental or ideal objects of the very highest order of thinkable abstraction or universality. In high degree, the consciousness of the mathematician qua mathematician is not concerned with either a self or objects. . .in higher degree than anywhere else, except perhaps in states of samadhi of a high order. Herein is revealed the power of pure mathematics as an instrument of consciousness-transformation on a very lofty level." (Wolff, 1973)

The implications of mathematics for the scientific study of consciousness are profound. First, it shows that a bona fide science of inner experience is not only possible, but already exists in our most rigorous and reliable of all sciences. Second, a consideration of the scientific method as it operates in mathematics suggests how the scientific method may be applied to other aspects of inner experience. Third, mathematics provides a precise and subtle descriptive language which may be just as powerful in the context of an inner science as it has proved to be in outer sciences. Fourth, mathematics has applications to inner science as an active instrument of investigation, and not just as a language of description. These possible uses of mathematics in a science of inner experience have been only touched on in this article with the hope that further research along these lines will bring insight into the scientific study of consciousness, both from within and without.

Bohr, Niels (1935),

'Can Quantum-Mechanical Description of Physical Reality be Considered Complete?', Physical Review, 48, pp. 696-702.

Cantor, Georg (1883),

Grundlagen einer allgemeinen Mannigfaltigkeitslehre. Ein mathematische-philosophischer Versuch in der Lehre des Unendlichen (Leipzig: B. G. Teubner).

Dauben, Joseph (1979),

Georg Cantor: His Mathematics and Philosophy of the Infinite (Princeton, NJ: Princeton University Press).

Ibn Arabi,

The Sufi Path of Knowledge, William C. Chittick tr., SUNY Press, 1989, p.67.

James, Jeffrey (1993),

'Boundary Mathematics', Master of Science thesis, University of Washington.

McFarlane, Thomas J. (1996),

'Integral Science: Toward a Comprehensive Science of Inner and Outer Experience', Journal of the Western Regional Chapter of the Alternative Natural Philosophy Association, 6 (2), pp. 4-15.

Nicholas of Cusa,

De Docta Ignorantia.

Plato,

Republic VII, 527e.

Plotinus,

Enneads V. v. 12.

Rucker, Rudy (1983),

Infinity and the Mind (New York: Bantam Books).

Spencer-Brown, G. (1969),

Laws of Form (London: George Allen and Unwin).

Tart, Charles T. (1972),

'States of Consciousness and State-Specific Sciences', Science, 176, pp. 1203-1210.

Wallace, B. Alan (1996),

Choosing Reality: A Buddhist View of Physics and the Mind (Ithaca, NY: Snow Lion Publications).

Wallace, B. Alan (1998),

The Bridge of Quiescence: Experiencing Tibetan Buddhist Meditation (Chicago: Open Court).

Wigner, Eugene (1960),

'The Unreasonable Effectiveness of Mathematics in the Natural Sciences', Communications in Pure and Applied Mathematics 13 (1).

Wilber, Ken (1979),

'Eye to Eye', ReVision, 2 (1); reprinted as Ch. 1 in Wilber (1990).

Wilber, Ken (1990),

Eye to Eye: The Quest for the New Paradigm (Boston, MA: Shambhala).

Wilber, Ken (1998),

The Marriage of Sense and Soul: Integrating Science and Religion (New York: Random House).

Wolff, F. (1944) [Merrell-Wolff, F.],

Pathways Through to Space (New York: Richard R. Smith); reprinted in Merrell-Wolff, F. (1994).

Wolff, F. (1973) [Merrell-Wolff, F.],

The Philosophy of Consciousness Without An Object (New York: Julian Press); reprinted in Merrell-Wolff, F. (1994).

Wolff, F. (1994) [Merrell-Wolff, F.],

Experience and Philosophy: A Personal Record of Transformation and a Discussion of Transcendental Consciousness (Albany, NY: SUNY Press).

Wolff, F. (1995) [Merrell-Wolff, F.],

Transformations in Consciousness: The Metaphysics and Epistemology (Albany, NY: SUNY Press).

[1]Fermat's Last Theorem, whose proof eluded mathematicians for hundreds of years, states that the equation aⁿ+bⁿ=cⁿ has no integer solutions for all positive integers n>2.